Andrew Gelman had an interesting post the other day, “Whither the ‘bet on the sparsity principle’ in a nonsparse world?” An excerpt:
Rob Tibshirani writes:
Hastie et al. (2001) coined the informal “Bet on Sparsity” principle. The l1 methods assume that the truth is sparse, in some basis. If the assumption holds true, then the parameters can be efficiently estimated using l1 penalties. If the assumption does not hold—so that the truth is dense—then no method will be able to recover the underlying model without a large amount of data per parameter.
I’ve earlier expressed my full and sincere appreciation for Hastie and Tibshirani’s work in this area.
Now I’d like to briefly comment on the above snippet. The question is, how do we think about the “bet on sparsity” principle in a world where the truth is dense? I’m thinking here of social science, where no effects are clean and no coefficient is zero…, where every contrast is meaningful—but some of these contrasts might be lost in the noise with any realistic size of data.
I think there is a way out here, which is that in a dense setting we are not actually interested in “recovering the underlying model.” The underlying model, such as it is, is a continuous mix of effects. If there’s no discrete thing to recover, there’s no reason to worry that we can’t recover it!
I had a comment which, while a bit tangential, I thought valuable. A lightly edited version:
LASSO (Tibshirani’s regression method which incorporates a sparsity-promoting regularization term) is presented in the context of linear mixing model. It’s formulated to deal with a scenario where the weight coeffs of the basis functions are sparse. When we ask “Is the world (non-)sparse?” to what extent are we asking “Is the world (non-)sparse in the context of a linear subspace model?” Linear subspace models are extremely useful but they’re not universal. Suppose your data can be described as a low-dimensional manifold which, when viewed globally, isn’t well accounted for using a subspace model? Would you call your data sparse or non-sparse?
And I provided two references:
C.M. Bachmann et al, “Improved Manifold Representations of Hyperspectral Imagery”
S.T. Roweis and L.K. Saul, “Nonlinear Dimensionality Reduction by Locally-Linear Embedding,” Science, vol. 290, pp.2323-2326, 22 Dec 2000.
I think I was posing good questions. To what extent does your data look nonsparse because of how you’re looking it? WWJTD?* Apparent nonsparsity could be a function of your vantage point. Why would that be any more or any less true for social science data than data than for physics or the physical sciences? (That’s not a rhetorical question.)
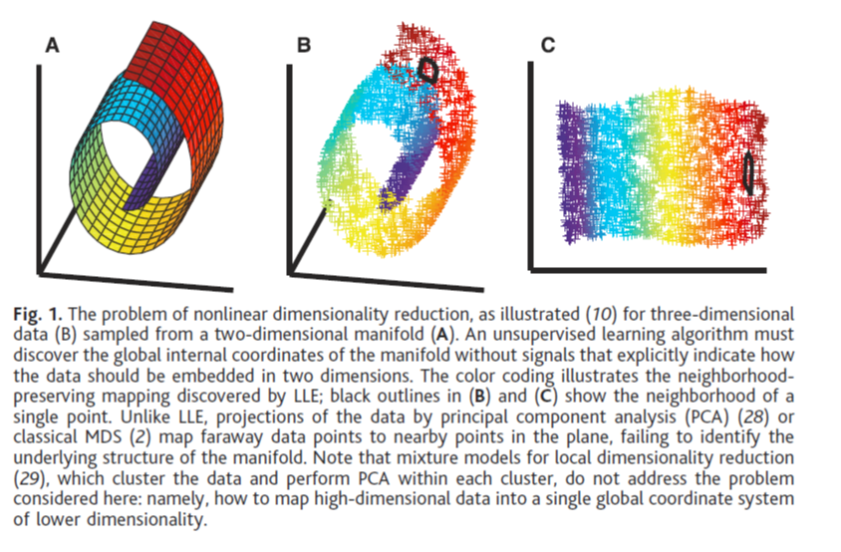
Here’s the “Swiss roll” data that Saul and Roweis analyze in their paper – their Figure 1:
The data occupies three dimensions in cartesian space but if you choose the right (nonlinear) coordinates it reduces to 2-D. If you constrain yourself to working with a linear representation then it takes more basis functions to capture the inherent structure of the data and, because of the number of basis functions required, you might conclude that the data is less sparse than it actually is. Data may be inherently nonsparse or it may simply appear nonsparse because you’re not looking at it correctly. Unfortunately, determining the vantage point from which it appears most sparse is non-trivial.
(Here’s a link to Swiss roll and other data useful for exploring nonlinear dimensionality reduction methods.)
The hyperspectral data that Bachmann and co worked with is much richer than the Swiss roll data. I linked to the Bachmann reference above because it’s a good short summary of his methodology and you can download it for free. His IEEE TGRS paper with the same authors, Exploiting Manifold Geometry in Hyperspectral Imagery, covers more ground but unless you’ve got a subscription to the journal you have to pay through the nose for it, $31. (I’ve seen similar characteristics in hyperspectral data I’ve worked with but am not at liberty to share those images here.) Worth a read if you can get for free – or at least far less than what IEEE is charging.
Anyhow, no responses to my comment on Andrew Gelman’s post. Usually I don’t care if my comments don’t generate a response but in this case I’m curious. Too far off-topic? No one familiar with the subject area? My comment so ridiculous that it doesn’t merit a response? All of the above? Who knows? Nothing but the sound of crickets chirping.