How to analyze data – short version

Posted on by

Inspired by a post on Andrew Gelman’s blog, The harm done by tests of signficance:

The first four steps to understanding cause and effect:

  1. Formulate your signal hypotheses, 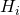H_i where i = 1, …, n.
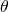  2. Fit your signal models to your data, \mathbf{x} .  Obtain model parameter values, \mathbf{\theta}, under each model.
  3. Reality-check your fit results. Does at least one of the fit models do a decent job of fitting the data?  (If 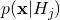p(\mathbf{x}|H_j) is crazy low for all of your signal hypotheses then either you’ve got a highly anomalous observation on your hands or your signal hypotheses do not include the one which gave rise to the data.)
  4. Compute posterior probabilities:

    \begin{equation*} p(H_j|\mathbf{x}) = \frac{p(\mathbf{x}|H_j) \cdot p(H_j)} { \sum_{i=1}^{n} p(\mathbf{x}|H_i) \cdot p(H_i)} \end{equation*}

Get through those steps and you may have a story to tell. That said, your estimates of effects and of which signal hypothesis best explains the observation are only as good as your data models, the associated probability distribution functions for measurement noise/covariance, and your estimates of p(H_i). Worth noting too that if your set of signal hypotheses is incomplete that could completely blow the p(H_j|\mathbf{x}) calculations.

I once heard someone remark, “Statistics is an arbitrary way of being reasonable.” With that in mind and the results of my fits in hand I might report the effect (and the associated uncertainty) corresponding to the largest p(H_j|\mathbf{x}), \mathbf{\theta}_i, or maybe I’d report the weighted value of the effect where p(H_j|\mathbf{x}) served as the weighting term, i.e.,

    \begin{equation*} \langle \theta_i \rangle = \frac{\sum_{i=1}^{n} {\mathbf{\theta}_i \cdot p(H_i)}}{\sum_{i=1}^{n} p(H_i)}} \end{equation*}

The goal should be to provide insight. There are a number of ways one could do that. If viewing one’s results from modestly different but seemingly reasonable perspectives yields significantly different conclusions then you should investigate and figure out why. Robust conclusions should be minimally sensitive to modest deviations from model assumptions and the fine points of how you interpret fit results.

Bottom line: The objective of any analysis should be to gain insight. Looking to p-values for Truth elevates dogma over insight.

PS To make Steps 2 and 4 above more Bayesian let

    \begin{equation*} p(\mathbf{x}|H_j) = \int p(\mathbf{x};\mathbf{\theta}) \cdot p(\mathbf{\theta}|H_j) \cdot d\mathbf{\theta} \end{equation*}

where  p(\mathbf{\theta}|H_j) is a prior for the distribution of \mathbf{\theta}.